-
[컴퓨터 비전] 이미지에서의 푸리에 변환 (Fourier Transform), 푸리에 변환의 의미Computer Vision 2024. 4. 13. 14:21반응형
푸리에 변환(Fourier Transform)
주기적인 함수는 여러 Frequency를 가지는 sin과 cos의 (무한)합으로 나타낼 수 있다.
* 푸리에 변환은 열 전도 등을 나타내기 위해 개발되었다. 초기에는 모서리(coner)가 있는 사각파 등을 나타내는 데에 한계가 있는것으로 보였지만, 모서리를 가진 그래프라도 근사하는 방법으로 푸리에 변환을 널리 사용하고 있다.
특히, 주기를 가진 함수를 푸리에 변환 할 수 있지만, 비주기 함수이더라도, 주기를 무한대로 본다면 푸리에 변환으로 나타낼 수 있다.
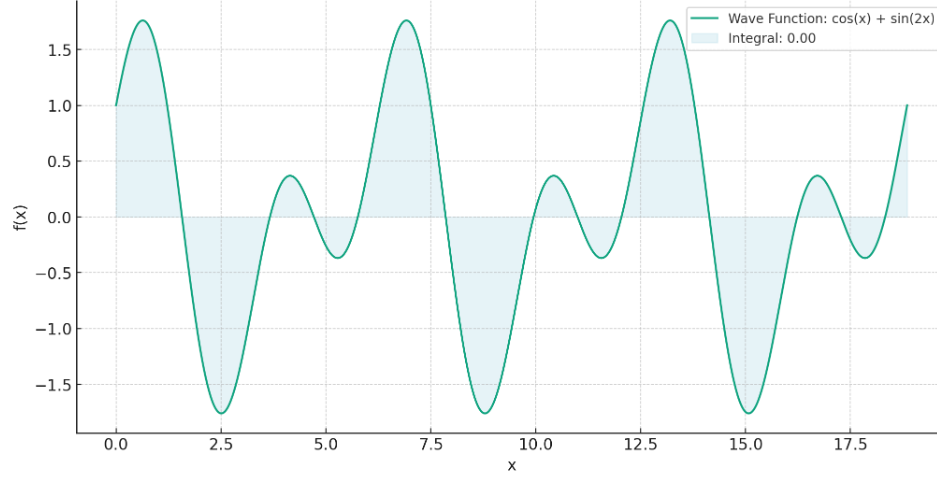
파동 1 (Chat GPT4 제작) 푸리에 변환의 기본 아이디어는, 같은 주파수를 가진 파동만 살리는 데에 있다. 위와 같이 파동이 있을 때 다른 주기의 파동을 곱하면, 적분한 값이 0이 된다.

주기성에 의해 적분한 값이 0이 된다. (Chat GPT4 제작) 반대로, 아래 그래프와 같이, 같은 주파수를 가진 함수는 적분해도 값이 0이 되지 않는다. (이는 내적의 개념과 유사하다.)

적분한 값이 0이 아니다. (Chat GPT4 제작) * 추가적으로 푸리에 변환 시 오일러 공식을 사용하여 cos과 sin을 포함한 식으로 표현할 수 있게 된다. 이를 복소수 평면에 그리면 신호의 위상을 구할 수 있다.
공간 신호 또한 시간 신호와 마찬가지로 푸리에 변환 될 수 있다.

시간 신호의 푸리에 변환 
공간 신호의 푸리에 변환 (왼쪽 이미지를 푸리에 변환 할 수 있다.) 아래 사이트에서 이미지를 넣으면 해당 이미지를 푸리에 변환한 결과를 확인할 수 있다.
https://www.myfourierepicycles.com
myFourierEpicycles.
myfourierepicycles.com lets the user draw their own fourier epicycle. The site also gives a brief explanation of the mathematics connecting fourier series and revolving epicycles.
www.myfourierepicycles.com
Fourier Transform Group
연속성 주기성 무한/유한 푸리에 Group 연속 input/output 주기 무한 Fourier Series 연속 input/output 비주기 유한 Fourier Transform 불연속 input/output 주기 무한 Discrete Fourier Series 불연속 input/output 주기 유한 Discrete Fourier Transform 연속 input/output
불연속 input/output비주기 무한 Discrete Time Fourier Transform (Transform은 finite / 위의 그룹 내에서는 Series는 infinite로 기억하면 편할 것이다 * 다른 예외나 오류가 있으면 댓글 부탁드립니다. *)
이외에도 FFT(Fast Fourier Transform)은 수학적으로 계산 효율이 높아서 컴퓨터 연산 시에 널리 활용된다.
Fourier Transform에서 평균이 나오는 값이, 제일 저주파라고 할 수 있다. ( $X(o)$ )
Discrete Fourier Transform (DFT)

Inverse discrete Fourier Transform (IDFT)

M=N일 경우,


Frequency Domain으로 변환 결과 푸리에 변환을 하여 주파수 범위에서의 그래프를 원하는 대로 변환하고, 그것을 다시 역푸리에 변환을 거쳐 돌려놓으면, 주파수 범위가 수정된 이미지를 얻을 수 있다.
반응형'Computer Vision' 카테고리의 다른 글